Racial Inequities in 2018 Boulder Police Discretionary Stops

Introduction

On May 1, 2019 the Boulder Police Department (BDP) released a (cleaned and processed) dataset containing data on all discretionary stops made by Boulder police in 2018. Discretionary stops make up only a fraction of Boulder police activity, with the vast majority of police interactions being non-discretionary, eg. where an officer was dispatched based on a 911 call or following a warrant. Approximately 66,400 police interactions are non-discretionary (per an in-person workshop on the data organized by the City of Boulder on May 6, 2019), whereas 8,209 are discretionary (per the released data).

The data were compiled on the recommendation of the consulting firm Hillard Heintz, who in 2016 were hired by the City of Boulder to perform an internal study of arrest and citation activity within BPD. In an analysis published alongside the BPD discretionary stop data, Hillard Heintz concluded that “black people are twice as likely as white people to be stopped at an officer’s discretion, and once stopped, they are twice as likely to be arrested”. To accompany these findings, the City of Boulder released an official report which contained several high-level takeaways, concerning what they understood to be the core points of the Hillard Heintz report:

1. The report represents only a single year of data and “cannot yet be put into context” (ie. trending up or down)
2. Small data sizes mean that small changes in stop or citation number may have meaningful effects in data trends
3. Laws and policies regulating discretionary action can have “significant positive effects”, but will require coordinated action
4. Racial differences in stop rates differ by base population (eg. residents vs nonresidents)

In my analysis of the data I found these summaries to be technically true, but highly conservative descriptors of what the data actually shows. Agreeing with the Hillard Heintz analysis of the dataset I find strong evidence that racial bias is occurring across all types of discretionary stop by BPD. Regardless of trend or context, in 2018 it was a real, urgent, and sizeable problem. If BPD were to stop black individuals at the same rate as white individuals (relative to the base population estimates given in the report) it would have constituted 220 fewer stops in 2018.

Breaking down the stop data by “stop reason” highlights some of the reasons why this bias occurs in the top-level. While different stop types affect Boulder residents and non-residents differently, for both groups the stop type exhibiting the largest bias was “municipal violations”. Speeding and traffic violations also made up a large component of the bias, as did stops where the listed reason was simply “suspicious”. Indeed, black individuals are stopped more frequently than white individuals in every type of stop listed except for “welfare checks” of non-residents, where BPD were slightly more likely to stop white individuals.

After confirming the Hillard Heintz results, I expand upon their methods by analyzing the outcomes of searches performed during discretionary stops. I find that black individuals who were searched for contraband were significantly less likely to have it than their white counterparts. This indicates that, on aggregate, BPD stop black individuals with a lower threshold of (productive) evidence. Critically, it implies that different perpetration rates cannot explain the apparent differences in other types of stop rates. Similar results also typically hold for white hispanic individuals, although base demographic information was not provided for this group and so the results are more limited. Black hispanic individuals were also largely absent from the dataset. It should be noted that race and ethnicity were assessed by the stopping officer.

Front Matter

Biased or unreasonable police stops are an injustice that needs to be redressed immediately, and the purpose of this analysis is to support that goal. With that said, before going any further it’s relevant to consider a quote from Candice Lanius’ excellent essay “Your Demand for Statistical Proof is Racist”:

Perhaps statistics should be considered a technology of mistrust—statistics are used when personal experience is in doubt because the analyst has no intimate knowledge of it. Statistics are consistently used as a technology of the educated elite to discuss the lower classes and subaltern populations, those individuals that are considered unknowable and untrustworthy of delivering their own accounts of their daily life. A demand for statistical proof is blatant distrust of someone’s lived experience. The very demand for statistical proof is otherizing because it defines the subject as an outsider, not worthy of the benefit of the doubt.

In short: nothing here is new, and if this analysis is the thing that changes your opinions on racist police practices in Boulder or elsewhere then you should be paying closer attention. Black lives matter.

About the Data

The original data is broken into two files: police_stop_data_main_2018.csv and police_stop_data_results_2018.csv. The first dataset contains a row for every individual discretionary stop made by Boulder PD. The columns in this dataset are:

"stopdate"      "stoptime"      "streetnbr"     "streetdir"    
"street"        "Min"           "sex"           "race"         
"ethnic"        "Year.of.birth" "enfaction"     "rpmainid"

We see columns for stop date, time, and duration (in minutes), as well as for race, ethnicity, and sex of the stopped individual as percieved by the reporting officer. We also have the column enfaction, which indicates if the stopped individual was a resident of Boulder or not, and the column rpmainid, which links each row to further information in the second dataset.

The structure of police_stop_data_results_2018.csv is slightly more complex. This file contains details on each stop listed in the main dataset, as well as the outcomes of each (if they exist). Let’s see what columns it has:

"appkey"   "appid"    "itemcode" "itemdesc" "addtime"

The appid column is used to link rows in results to rows in main (through the rpmainid column). A big difference here is that each value of rpmainid appears only once in main, whereas a single appid might be listed in multiple rows in results, corresponding to multiple outcomes of the same stop. The appkey column contains one of seven different values, ‘RPT1’ through ‘RPT7’, which indicate what kind of information is contained in the row:

Appkey	Data
RPT1	Stop type
RPT2	Stop reason
RPT3	Search conducted
RPT4	Search authority
RPT5	Contraband found
RPT6	Result of stop
RPT7	Charge issued

The corresponding info is then stored in itemdesc. Each pair of appid and appkey might be listed in multiple rows, eg. if there’s more than one reason for the stop. This is not a very convenient data stucture. It would be far better if all of the information was present in a single dataset, and if each row corresponded to exactly one stop, ie. if the data was tidy. Fortunately my friend Sam has gone ahead and done just that. Sam one-hot encoded each appkey/infodesc pair, ie. assigned each pairing its own column, with a 1 in that column indicating that the appkey for that stop had the infodesc value.

Data Analysis

A useful resource that I relied on while performing this analysis was Methods for Assessing Racially Biased Policing by Ridgeway and MacDonald. They define two approaches for determining police bias, “benchmark analysis” and “outcome tests”. I use both here, beginning with a benchmark analysis of all discretionary stops.

Assessing Top-Level Bias

The basic logic of a benchmark analysis compares the percentage of stopped individuals of race R to the underlying demographics of the larger policed popilation. If race R is Y% of the population, but comprises X%>>Y% of the police stops, then this is taken to indicate that race R is over-policed (or vice versa). This approach faces a number of challenges however, largest among being that in a city like Boulder, the total policed population is a superset of the census population (ie. “residents”). Police also interact with commuters, students, and unhoused people who are not represented in the Boulder census. The City of Boulder therefore put in a lot of work estimating demographic information about this larger community, and their findings can be found in their 2018 Annual Report. To start my analysis I’m just going to pull their population totals and demographic breakdown information and enter it manually, so that I can repeat and confirm their conclusion that black individuals are stopped more frequently than white indiviuals, per population size. Only race was included in the demographic information, not ethnicity (unlike in the discretionary stop data), so there are no baselines for white or black hispanic individuals and therefore are excluded from this first analysis.

Let $N_R$ denote the number of individuals of race R in the Boulder policed population. I assume that every such individual has an equal probability of being stopped by BPD, denoted $p_R$. This is absolutely a “first-order” assumption and is highly suspect; even given race, an individual’s location, behavior, appearance, etc. all likely effect the probability of being stopped by BPD. For each R, the value $N_R$ is set equal to the estimate provided by the city of boulder

From the BPD discretionary stop data I calculate $y_R$, the number of stops which occurred, where the stopped individual was of race $R$. This is simply the number of occurences of each race category in the race column of the tidied data. Note that a single individual may have been stopped multiple times, and in that case would appear as two or more rows in the tidied data. I do not account for multiple occurences in this, or any model in this analysis. Below are the total number of stops and demographic information for white (‘W’), black (‘B’), asian (‘A’), and indigenous (‘I’) individuals:

Race	Total Stops ($y_R$)	Percent Stops	Percent of Pop.	Total Pop. ($N_R$)
A	310	0.04	0.06	9154.942
B	353	0.04	0.02	2743.798
I	36	0.00	0.01	2743.798
W	7425	0.90	0.91	2743.798

As indicated in the Annual Report, there does appear to be some mismatch between stop rates and demographic representation. But just from this table it’s not fully clear if these differences are meaningful, or if they just represent noise. To quantify the uncertainty in the above totals, I perform a basic Bayesian analysis. Given the above $y_R$ and $N_R$, as well as the previous assumptions, we have that $y_R$ is binomially distributed with paramters $N_R$ and $p_R$. Placing a uniform prior on each of the $p_R$ then gives a Beta-distributed posterior density over the $p_R$: $$ P[p_R|y_R,N_r] \propto p_R^{1+y_i}(1-p_R)^{1+N-y_i} $$

Below are boxplots for the posterior over each of the $p_R$:

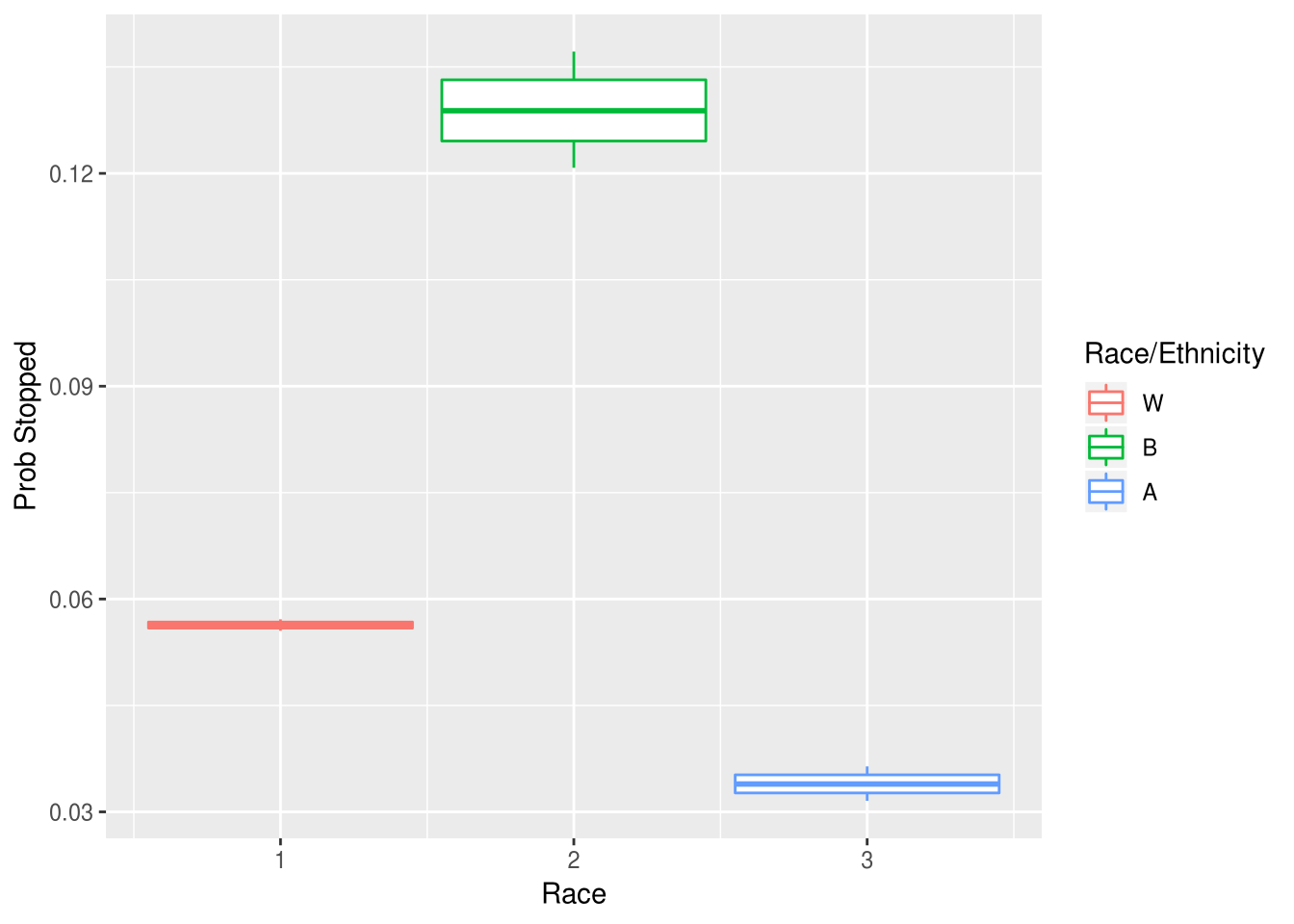
Since the boxplot for each posterior density exhibit substantial amounts of separation it’s clear that there are serious racial differences between the probabilities of experiencing a discretionary stop. Asian and white individuals seem to have a similarly, low probability of being stopped, however black individuals are substantially more likely to have been stopped (relative to the population demographics). Let’s now dig in on what is contributing to this discrepancy.

Most Biased Search Reason?

Every stop in the dataset lists the reason the officier initiated the stop. Some of the given reasons seem especially likely to be exhibit differences across races (eg. one stop reason is that the officer was “suspicious”). I therefore repeated the above analysis for subsets of the data corresponding to each different stop reason. I then ranked each stop reason by the number of “extra individuals stopped for that reason”. This was calculated as the scaled difference $(\bar{p_B} - \bar{p_W})N_B$, where $\bar{p_B}$ is the posterior median probability that BPD stopped a black individual (respectively, white individual). This index can be interepreted as the number of additional black individuals stopped due to a raial discrepancy in stop rates. When this index is positive and large it indicates a potential source of the difference in top-level stop rates. Since different populations might be experience different stop reasons (eg. commuters are more likely than residents to be stopped for speeding), I performed separate analyses on the resident and non-resident populations, as well as on both populations together:

Reason	Bias (All)	Bias (Res.)	Bias (Non-res.)
municipal.violation	78.5	13.6	62.8
traffic.speeding	42.2	7.7	34.2
traffic.reckless.careless	22.9	6.6	17.0
equipment.violation	22.3	9.0	13.2
traffic.right.of.way.violation	22.2	6.5	16.6
suspicious	17.0	5.4	11.4
state.violation	6.2	3.0	3.9
traffic.reddi.observed.pc	5.8	.5	6.0
traffic.parking.violation	2.4	2.6	.5
noise.violation	1.5	1.6	.6
welfare.check	-.2	1.2	-.7

We see that many stop reasons in the dataset exhibits a large and significant anti-black bias. In terms of “extra individuals stopped” the bias is largest for non-resident stops, although the leading stop types appear to be similar for both categories (ie. municipal violations and speeding or other traffic violations). The relatively high bias in the “suspicious” stop reason is also telling. That black individuals are viewed with elevated suspicion seems further underlined by the fact that the only time BPD are more likely to stop a white individual is when performing a non-resident “welfare check”. In total, over 220 “extra” black individuals are policed per year (ie. 220 people are subject to discretionary stops who would not have been if black individuals were policed at the same rate as white individuals).

Outcome Testing Search Results

A frequent criticism of benchmark analyses like the above argues that racial differences in stop rates may reflect racial differences in the underlying crime rates, and thus are justified police practice. One way that we can assess whether this claim is consistent with the data is by performing an outcome test.

Outcome tests originated in the economics literature to test whether loan officers were discriminating against black applicants. The idea (in its original use) was to look at whether black individuals who did recieve home loans defaulted at a lower rate than their white counterparts. If the data showed that this was the case (and it did), then it indicated that loan officers were holding black applicants to a higher standard financial standard than white applicants. We can apply a similar logic here by looking at the rates at which discretionary police searches turn up contraband (the "hit rate"). If black individuals who are searched are less likely to have contraband than white individuals who are searched, it suggests that police are searching black individuals with a lower threshold of evidence, ie. that skin color is a factor in their decision to search beyond the simple demographics of crime. This test is not perfect, but the case where this test fails is not favorable to the argument that white populations are less criminal.

We can apply the same basic modeling framework as in the benchmark test to perform the outcome test. Now, however, let $N_R$ represent the total searches performed on individuals of race $R$ nd let $y_R$ be the number of searches which turned up contraband. Let’s plot the posterior density for both the probability that an individual is searched, and that a search turns up contraband:

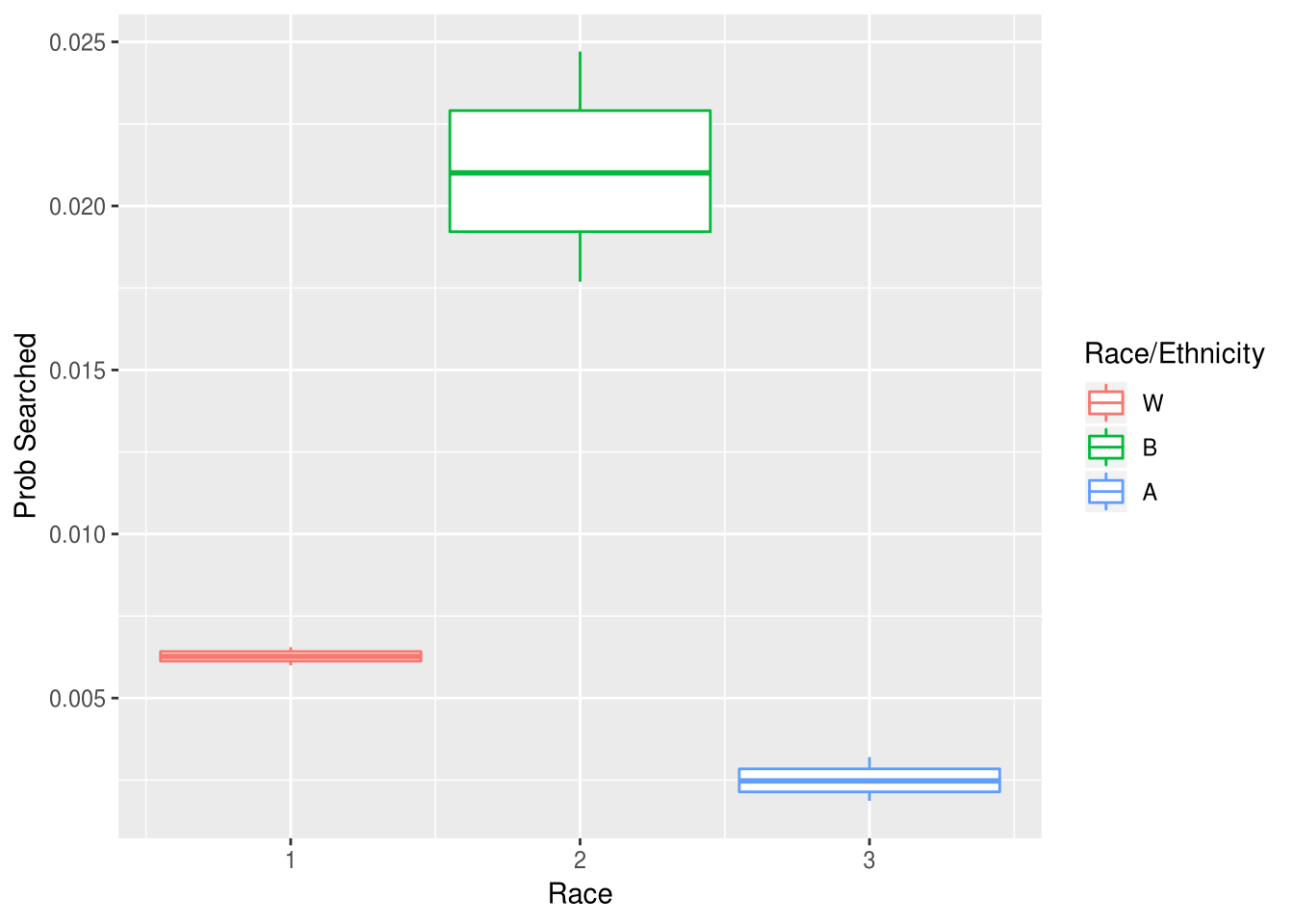
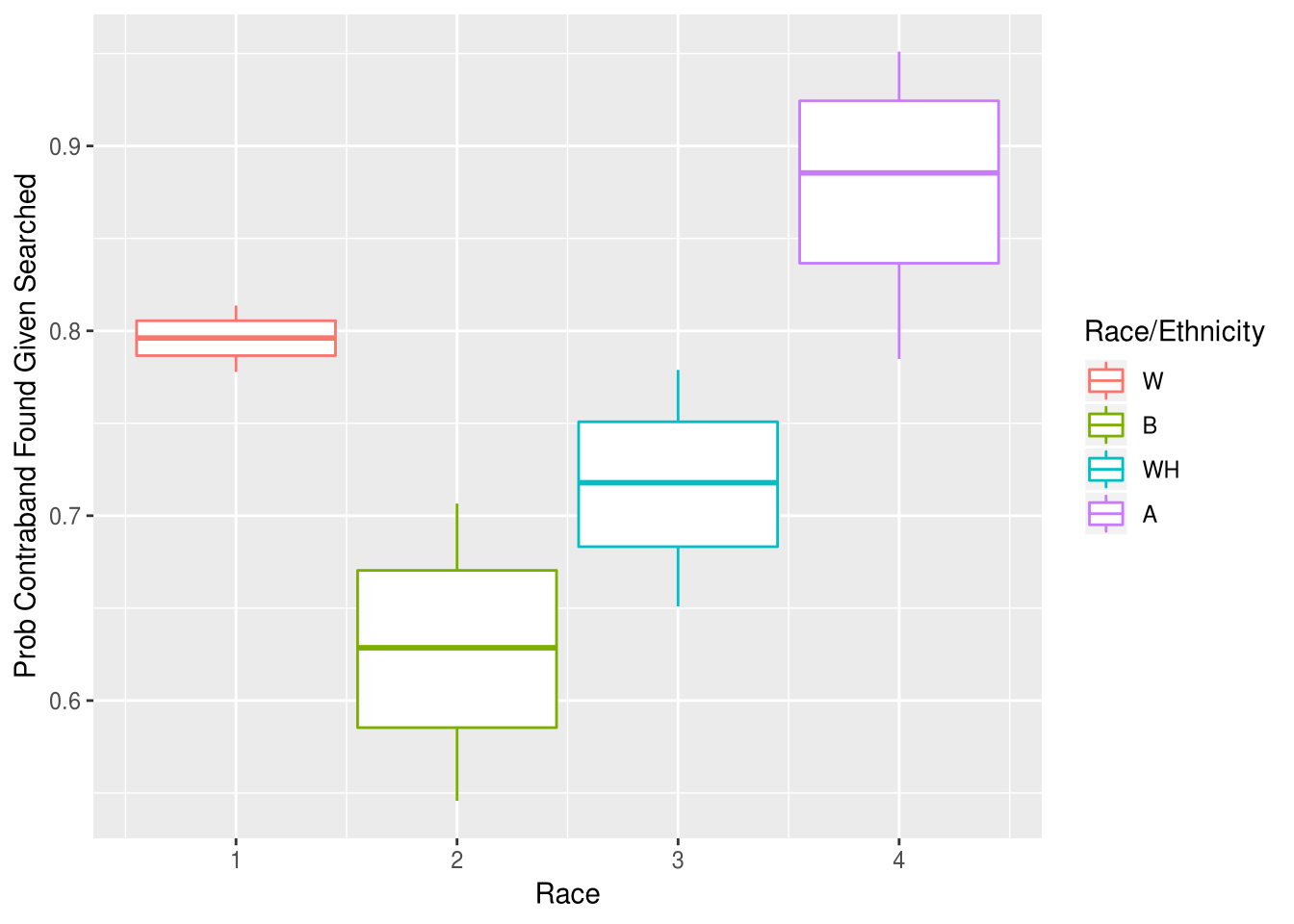
Black individuals are the most likely to be searched, but the least likely to carry contraband, among those searched. The discrepancy in outcome holds for both residents and non-residents, and for consent and non-consent searches (for brevity those results are not plotted, but code can be made available on request). Similar to the previous analysis, we can also estimate the number of “extra searches” of black individuals (ie. the number of searches of non-contraband possessing black individuals which would not have been performed if black and white individuals were searched at similar rates). Assuming that white individuals are not more likely to carry contraband than black individuals (an assumption that could easily be up for dispute, but which does not directly bear on the argument here) the different standard of evidence with which BPD conducts searches resulted in around 57 “unnecessary” searches of black individuals. In other words: to get equal rates of contraband discovery between black and white individuals, BPD would need to have searched 57 fewer innocent, black individuals.

Outcome Tests of Speeding Stops

According to my top-level analysis of stop rates, one of the most biased stop reasons was speeding stops. We can apply an outcome test here as well, to asses whether this difference reflects real differences in perpetration rates. I find that, despite being cited less for speeding than other races, black drivers were arrested more. Furthermore, of those arrested during a speeding stop, black drivers were ultimately more likely to have the charge overturned.

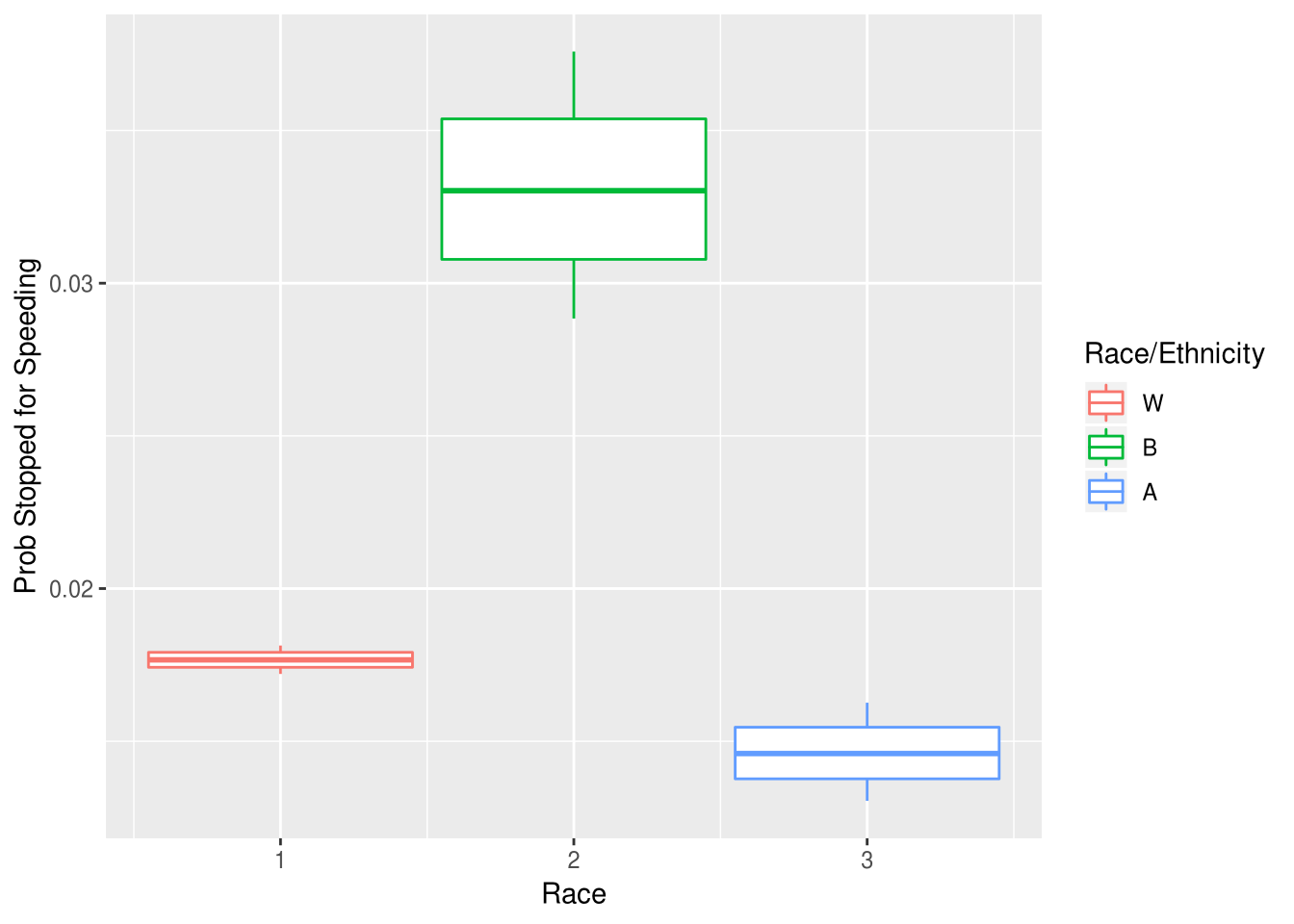
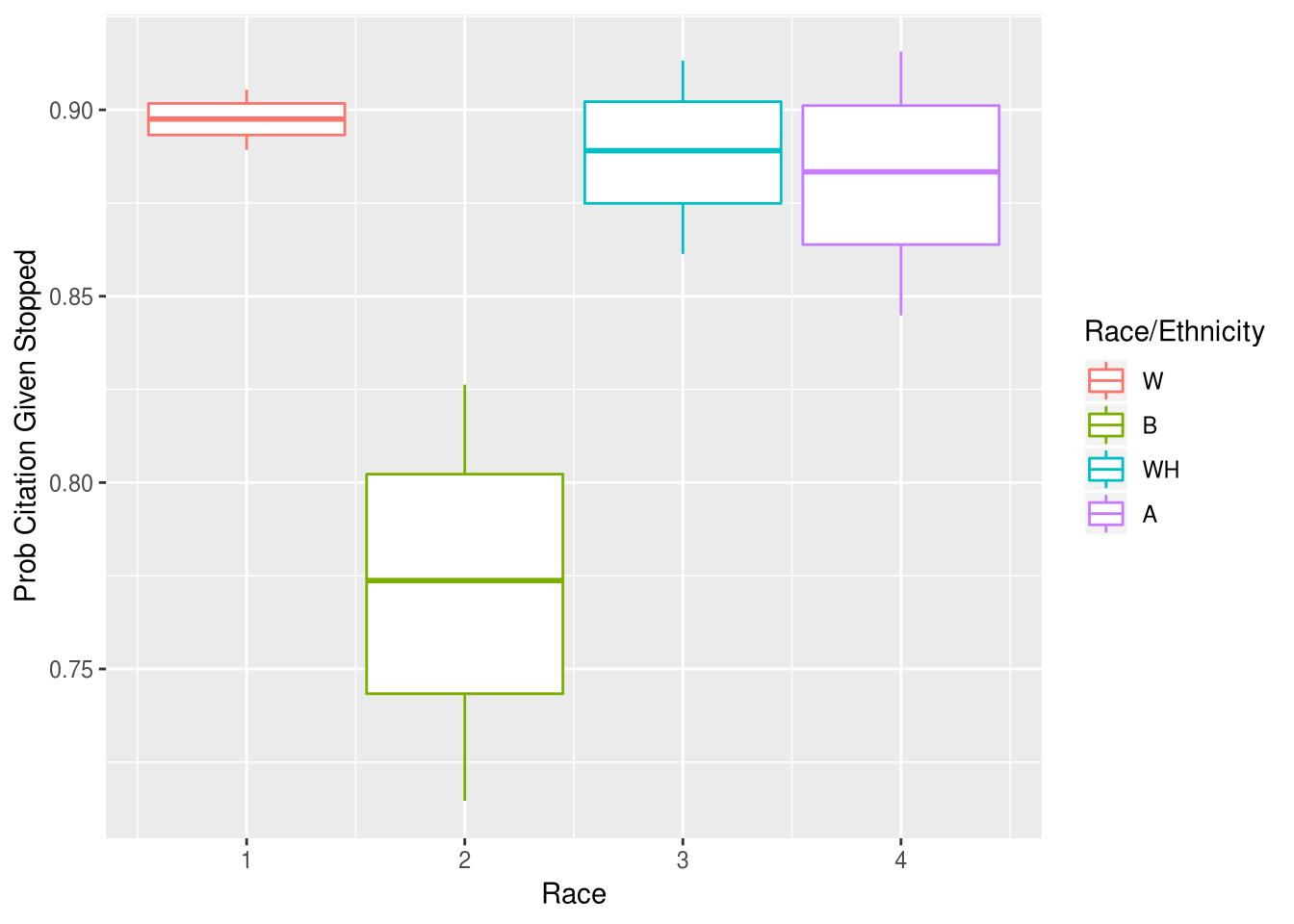
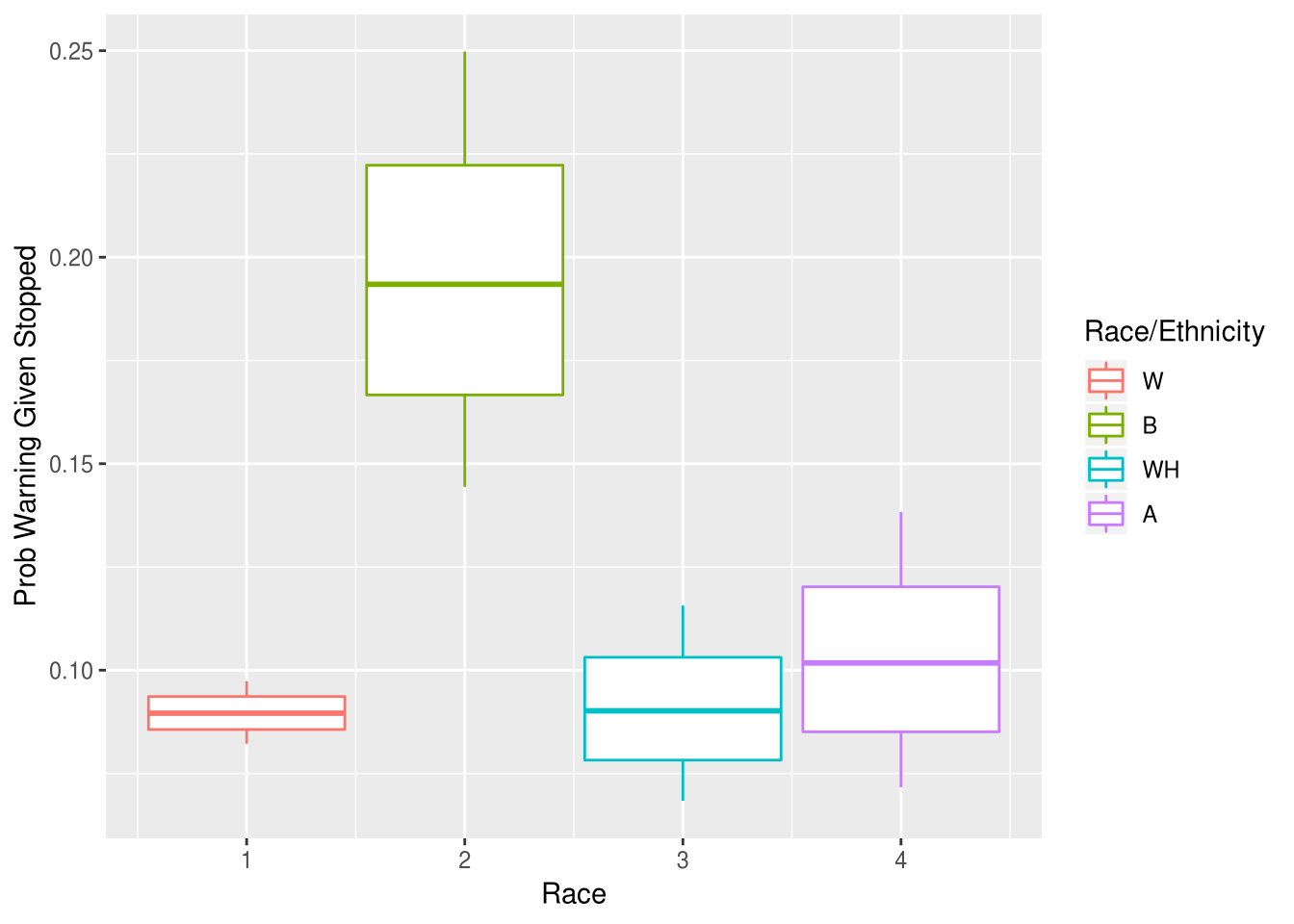
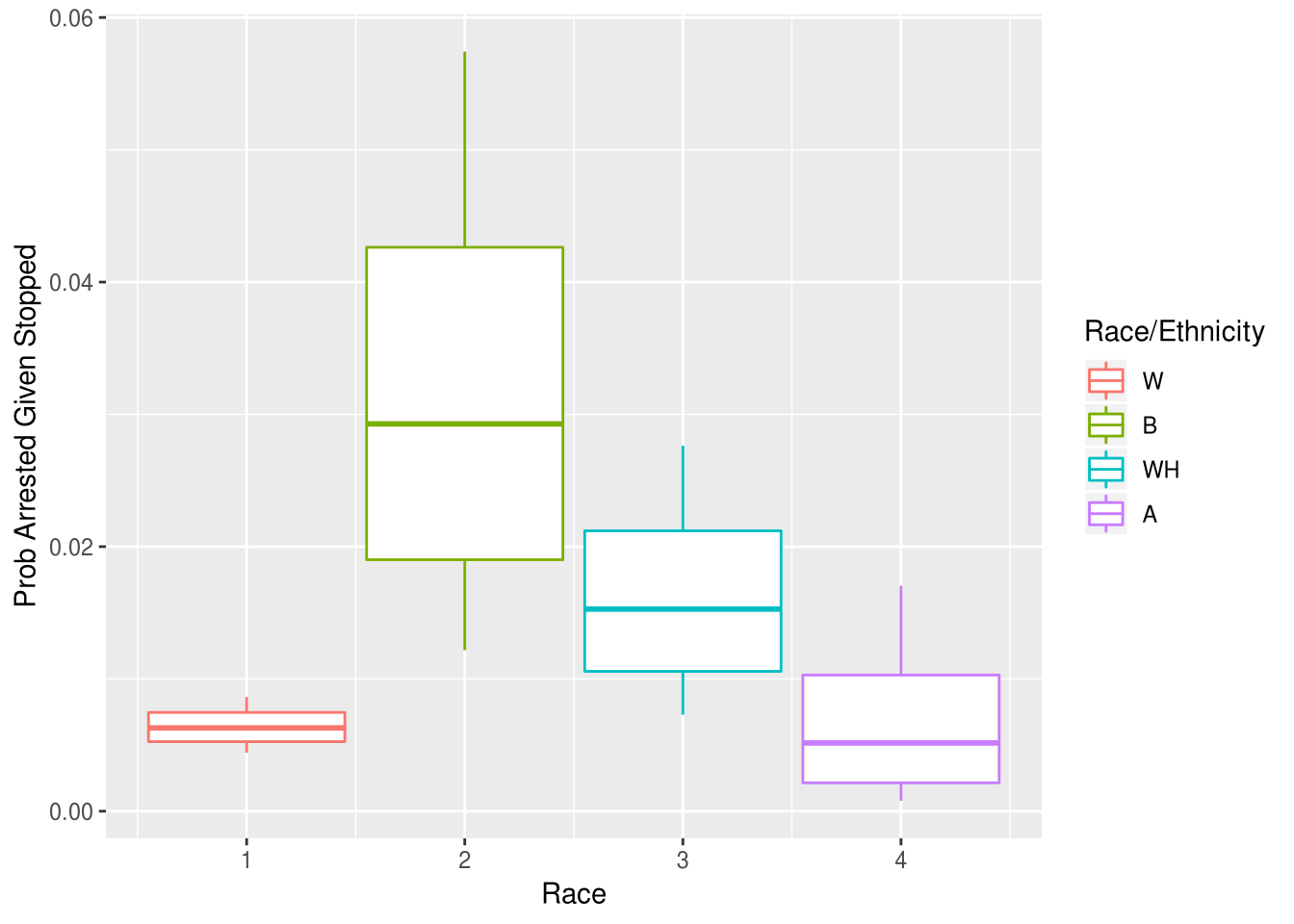
An outcome test does struggle here a little, because the outcome (the issuance of a speeding citation) is also a decision at the stopping officer’s discretion (versus in the case of search outcomes, where the contraband is either present or not). If black drivers are cited less it could be the case that Boulder PD are more lenient towards black drivers. Indeed we do see that black drivers are more likely to recieve a warning than other drivers. However it could also be the cases that that black drivers are being stopped at lower driving speeds which don’t justify a ciation (maybe 1-10 MPH over the limit), which would be more consistent with the other results in this analysis. A more complete dataset could clarify this ambiguity: if we had access to the recorded driving speed of the stopped drivers we could apply the test to those values, rather than just the binary cited/not cited outcome.

Conclusion

This analysis is really just a first look at the ways that BPD may be treating its policed population unequally across race. Due to limitations of the dataset we were unable to answer questions regarding police activity towards the unhoused, nor get a complete picture of what’s going on with speeding stops. Nevertheless, by almost every measure considered, black individuals in Boulder are subjected to elevated suspicipion and surveillance by the police department. At the most cynical level, this represents an inefficiency in our local government. That this increased police scrutiny results in fewer productive searches and citations indicates that BPD is misallocating its time and resources towards innocent black people. Far more importantly, however, is the real harm that this data indicates is happening. We have the right against unreasonable search and seizure, and this dataset indicates that in 2018 BPD violated that right among black individuals who lived or traveled through our community. That the City of Boulder and its citizens are allowing this to occur is entirely unacceptable and any delay in redressing it prolongs a serious injustice.